إذ كنت تمتلك هاتفا من نوعية «الآيفون»، فعليك معرفة أن الزر الجانبي في الهاتف لا يقتصر على قفل الشاشة فحسب، إذ قد يجهل البعض أنّ هذا الزر يخفي على الأقل أربع حيل مفيدة للغاية، فمن خلال استخدام المزيج الصحيح من الإعدادات والنقرات المتعلقة بزر القفل، يمكنك جعل الهاتف يقوم ببعض الأشياء المفاجئة، بما في ذلك مساعدتك على تجنب دوار الحركة.
اختصار إمكانية الوصول
وترتبط الحيل الثلاث الأولى المتعلقة بزر القفل الجانبي في هواتف آيفون جميعها بميزة تسمى اختصار إمكانية الوصول، إذ يتيح لك هذا تعيين وظائف مختلفة للزر الجانبي، ويجري تنشيطها جميعًا بنقرة ثلاثية سريعة، فهناك العشرات من الخيارات، ولكن يظل خيارات مفيدة بشكل خاص من خلال الانتقال إلى الإعدادات ثم إمكانية الوصول، والضغط على اختصار إمكانية الوصول، وفقًا لصحيفة «ذا صن» البريطانية.
ومن خلال الضغط على هذا الاختصار، ستشاهد قائمة طويلة من الميزات التي يمكنك إضافتها إلى الزر الجانبي، وسيظل خيار الضغط مرة واحدة على الزر الجانبي صالحًا لقفل جهاز iPhone الخاص بك، ولكن إذا قمت بالنقر فوقه ثلاث مرات، فسوف يقوم بتنشيط الميزة التي تختارها، وإذا قمت باختيار خيارات متعددة، فإن النقر الثلاثي سيؤدي إلى فتح قائمة منبثقة تحتوي على اختياراتك، ما يتيح لك النقر فوق الخيار الذي تريده في ذلك الوقت.
ومن أفضل الميزات التي يمكنك الاستمتاع بها بواسطة زر القفل الجانبي، هي ميزة أصوات الخلفية الخاصة بـiPhone، والتي يمكن أن تساعدك على التركيز أو حتى النوم، إذ يمكنك اختيار صوت الخلفية الافتراضي من الإعدادات، ثم إمكانية الوصول، والانتقال إلى الصوت والفيديو وبعدها الأصوات الخلفية، ولا يقتصر الأمر على النوم فقط؛ إذ يمكنك تشغيل الأصوات في الخلفية أعلى ملفات البث الصوتي وأنواع أخرى من الوسائط أيضًا.
خيار مكافحة الغثيان
أما الخيار الثاني هو Vehicle Motion Cues، والذي صُمم لمكافحة الغثيان الناتج عن استخدام جهاز iPhone الخاص بك أثناء وجودك في سيارة متحركة، فإذا كنت تعاني من عدم الراحة عند استخدام جهاز الآيفون أثناء ركوب السيارة أو أي مركبة أخرى على الطريق، فيمكنك تشغيل إشارات حركة السيارة، وهي إشارات تظهر على الشاشة قد تساعد في تقليل دوار الحركة أثناء القيادة، بحسب شركة Apple، وتظهر إشارات حركة السيارة كنقط متحركة على حواف الشاشة تمثل كيفية تحرك السيارة دون التدخل في ما تفعله على iPhone.
وتشير شركة Apple إلى أنّه ليس هناك ضمان بنسبة 100% أن دوار الحركة الذي تعاني منه سيختفي، ولكن الأمر يستحق المحاولة في المرة المقبلة عندما تكون راكبًا.
خاصية المكبر
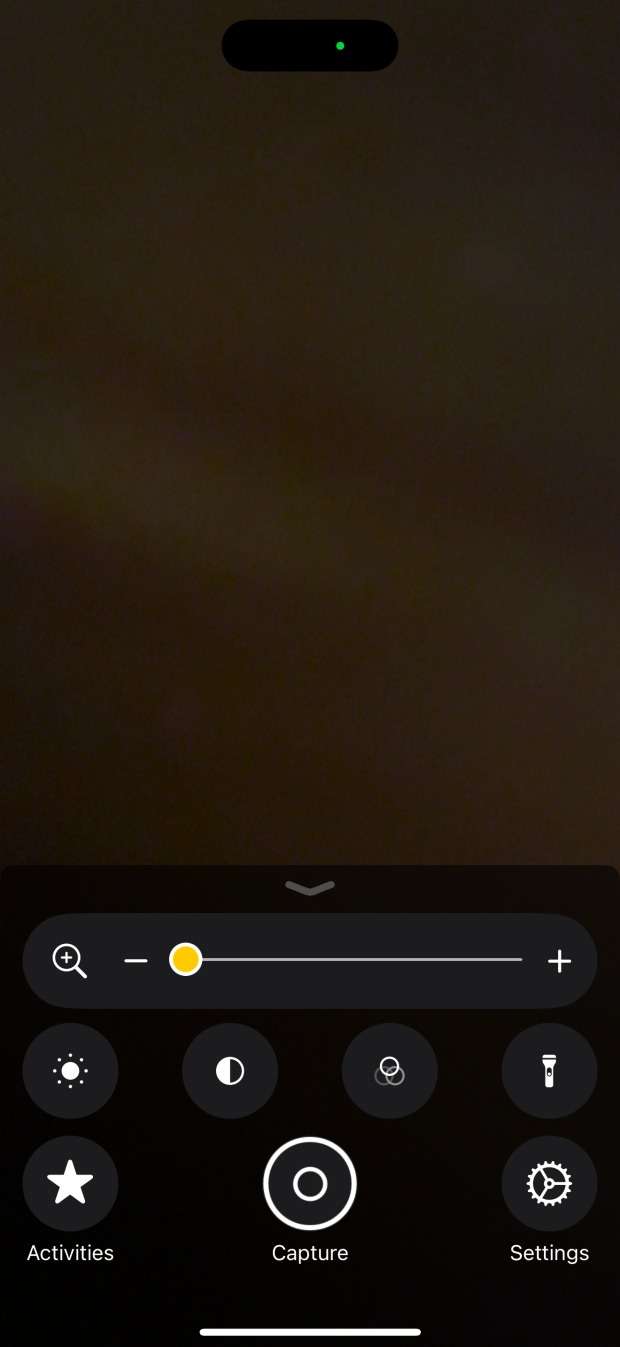
أما ثالث هذه الخيارات هو المكبر، فعند تفعيله والضغط عليه يعرض نسخة مختصرة من كاميرا جهاز iPhone الخاص بك والتي صممت خصيصًا للتكبير على الأشياء الصغيرة، وذلك عندما تحاول قراءة بعض تعليمات المنتجات، أو النظر إلى جزء صغير من النص الموجود على الجزء الخلفي من أحد الأجهزة، أو مجرد تكبير صورة مفصلة رأيتها في كتاب، لذا فإنّ القدرة على سحب العدسة المكبرة بسرعة كبيرة قد تكون مفيدة حقًا.
خيار خدمات الطوارئ
أما الحيلة الرابعة هي ميزة منفصلة تمامًا مرتبطة بخدمة Emergency SOS التي تقدمها Apple، وذلك من خلال الانتقال إلى الإعدادات ثم الضغط على SOS الطوارئ، ثم قم بتشغيل ميزة الاتصال بخمسة ضغطات على الأزرار، وعندما تضغط بسرعة على الزر الجانبي خمس مرات، سيؤدي ذلك إلى تشغيل استجابة SOS الطارئة على جهاز iPhone الخاص بك، وسيؤدي هذا إلى بدء العد التنازلي وسيصدر صوت تنبيه، وبمجرد انتهاء العد التنازلي، سيقوم جهاز iPhone الخاص بك تلقائيًا بالاتصال بخدمات الطوارئ.
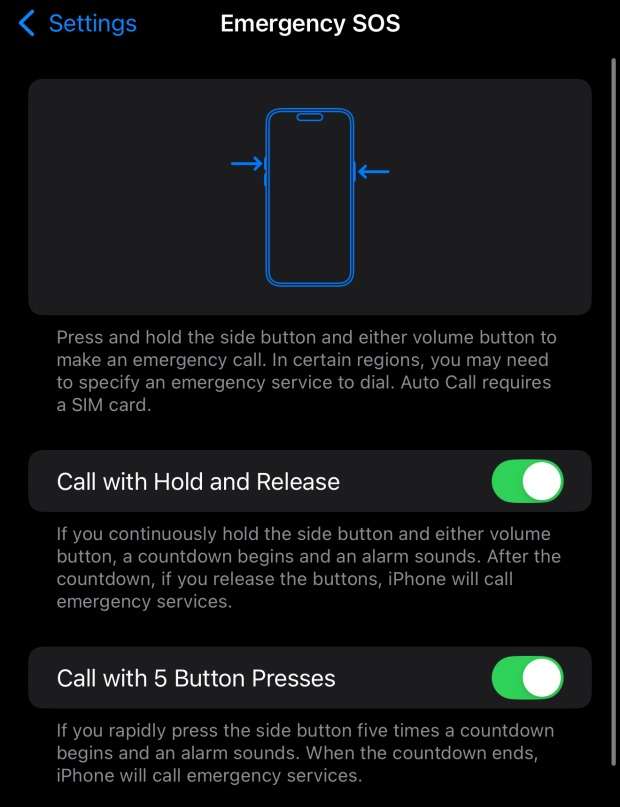
كما يمكنك أيضًا إعداده لتنبيه جهات الاتصال في حالات الطوارئ والتي يمكنك إضافتها في صفحة الإعدادات نفسها، وهي طريقة سريعة جدًا للاتصال بخدمات الطوارئ دون الحاجة إلى الانتقال إلى تطبيق الهاتف وكتابة رقم.
































