02:06 م
الأربعاء 22 يناير 2025
بي بي سي
عادت مدينة جنين الفلسطينية ومخيمها إلى الواجهة من جديد، بعدما بدأ جيش الاحتلال الإسرائيلي عملية عسكرية جديدة أطلق عليها اسم “السور الحديدي”، أمس الثلاثاء، أدت لاستشهاد 10 فلسطينيين وإصابة 40 آخرين. ودفع جيش الاحتلال فجر اليوم الأربعاء بتعزيزات عسكرية كبيرة إلى مدينة جنين ومخيمها.
وأكدت مصادر في جنين أن غالبية الشهداء هم من المدنيين.
وأعلنت “كتيبة جنين” التّابعة لسرايا القدس عن تفجير عبوة ناسفة أرضية من نوع ( kj37) بناقلة جند إسرائيليّة في “طلعة الغبز” موقعين قتلى وجرحى في صفوف جنود الاحتلال.
وقال جيش الاحتلال الإسرائيلي إن قوات كبيرة ستشارك في عملية “السور الحديدي”، بما في ذلك الوحدات الخاصة و”الشاباك” و”حرس الحدود”، “وستستمر العملية طالما كان ذلك ضرورويًا”.
فماذا نعرف عن جنين المدينة ومخيمها؟
جنين: المدينة
تعتبر مدينة جنين أكبر مدن محافظة جنين، وتقع شمال الضفة الغربية التابعة للسلطة الفلسطينية. تبعد المدينة مسافة 75 كيلومترًا عن القدس من ناحية الشمال، وتطل على غور الأردن من ناحية الشرق، وتقع على السفح الشمالي لجبال نابلس على الجانب المطل على مرج بن عامر.
وجنين مدينة قديمة أسسها الكنعانيون، وقد دخلت تحت الحكم العثماني في القرن السادس عشر، ثم الحكم المصري لفترة وجيزة خلال القرن التاسع عشر، بعد أن نجح إبراهيم باشا ابن والي مصر محمد علي باشا في طرد العثمانيين منها.
وفي القرن العشرين، خضعت المدينة للانتداب البريطاني، ثم غادرها الإنجليز في عام 1948، وهو العام ذاته الذي شهد قيام دولة إسرائيل.
في عام 1949، آلت المدينة إلى حكم الإدارة الأردنية، ودخلت هي وباقي أنحاء الضفة الغربية في اتحاد مع المملكة الأردنية الهاشمية. وفي عام 1964، أصبحت مركزا للواء جنين التابع لمحافظة نابلس.
وبقيت المدينة تحت الحكم الأردني حتى احتلالها من قِبل إسرائيل خلال حرب عام 1967.
استمر ذلك الوضع حتى عام 1995، عندما خضعت مدينة جنين لإدارة السلطة الفلسطينية التي تأسست عام 1994 بموجب اتفاق غزة-أريحا. وقد أصبحت مدينة جنين منذ ذلك الحين مركزًا لمحافظة جنين.
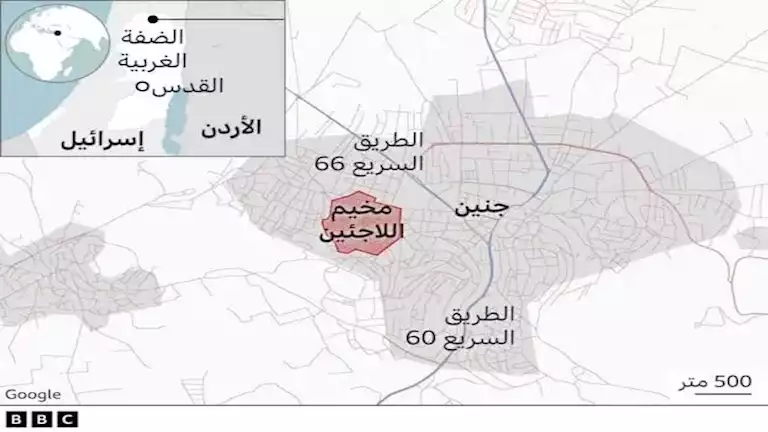
جنين: المخيم
تأسس مخيم جنين عام 1953 ضمن حدود بلدية جنين، ويقع حاليًا ضمن مساحة من الأرض تبلغ 0.42 كم مربع.
ينحدر سكان المخيم من منطقة الكرمل في حيفا وجبال الكرمل، وكان الغرض من إنشائه هو إيواء الفلسطينيين الذين نزحوا خلال الحرب التي استمرت من عام 1948 إلى عام 1949 في أعقاب إعلان قيام دولة إسرائيل.
ووفقًا لوكالة الأمم المتحدة لغوث وتشغيل اللاجئين الفلسطينيين “أونروا”، فإن عدد سكان المخيم يبلغ 14000 نسمة في الوقت الحالي، يعيشون في تلك المساحة الصغيرة التي تقل عن نصف كيلومتر مربع.
يعمل العديد من سكان المخيم في القطاع الزراعي بالمناطق المحيطة بجنين، ويعاني المخيم من نسبة مرتفعة للغاية من البطالة.
وقد شهد المخيم الكثير من الصراعات المسلحة، مثله مثل باقي الأراضي الفلسطينية، خلال الانتفاضتين الفلسطينيتين الأولى عام 1987 والثانية عام 2000.
ولربما كان الحدث الأبرز الذي شهده المخيم هو حصار القوات الإسرائيلية له في أبريل عام 2002، والذي وصفه الرئيس الفلسطيني الراحل ياسر عرفات بـ “جنين غراد”، نسبة إلى حصار مدينة ستالينغراد الروسية التي صمدت أمام الحصار الألماني الطويل لها خلال الحرب العالمية الثانية.
وبعد سلسلة من التفجيرات التي نفذها مقاومون فلسطينيون – العديد منهم من جنين – داخل إسرائيل، شنت القوات الإسرائيلية اجتياحًا شاملًا فيما عرف بـ “معركة جنين”، مما أسفر عن استشهاد ما لا يقل عن 52 مقاومًا ومدنيًا فلسطينيًا وقتل 23 جنديًا إسرائيليًا. وقد استمرت العملية 10 أيام.
وتقول الأمم المتحدة إن العملية، التي أطلقت عليها إسرائيل اسم “السور الواقي”، أسفرت عن تدمير 150 بناية، في حين أصبح العديد من المباني الأخرى غير صالح للعيش فيه، وهو ما أدى إلى أن أصبحت حوالي 435 عائلة بلا مأوى.

“كتيبة جنين”
بعد سنوات من الهدوء، تصدر مخيم جنين عناوين الأخبار مرة أخرى في عام 2021 مع ظهور جماعة مسلحة جديدة هي “كتيبة جنين” التي يقول مراقبون إنها تضم عناصر من تنظيمات الجهاد الإسلامي وحركتي فتح وحماس، إضافة إلى عناصر لا تنتمي إلى أي تنظيمات سياسية.
ويعتقد أن مؤسس الكتيبة هو جميل العموري، الذي اغتالته إسرائيل في 10 يونيو عام 2021، داخل المخيم، وكان العموري قياديًا بارزًا في سرايا القدس، الجناح العسكري لحركة الجهاد الإسلامي.
العدد الحقيقي لأفراد كتيبة جنين غير معروف، ولكن العشرات منهم ظهروا في عروض عسكرية أو أثناء جنازات مقاتلين سقطوا خلال اشتباكات مع قوات الاحتلال الإسرائيلية.
ويستخدم أعضاء الكتيبة قنابل بدائية محلية الصنع خلال الاشتباكات التي تقع بينهم وبين قوات جيش الاحتلال الإسرائيلي.

وفي عام 2022، شهدت مدينة جنين ومخيمها حملات عسكرية إسرائيلية متكررة، حيث قالت إسرائيل إن عددًا من عناصر المقاومة المسؤولين عن مقتل إسرائيليين خرجوا من منطقة جنين.
وكانت مدينة جنين ومخيمها وقراها أحد الأهداف الأساسية لعملية “كاسر الأمواج” التي أطلقتها إسرائيل في بداية أبريل 2022 بعد سلسلة هجمات نفّذها عناصر من المقاومة الفلسطينية في إسرائيل والضفة الغربية. وقالت إن هدفها هو منع وقوع عمليات فلسطينية مسلحة واعتقال من يخططون لتنفيذها.
وفي 11 مايو من العام ذاته، استشهدت شيرين أبو عاقلة مراسلة قناة “الجزيرة” الإخبارية القطرية بالرصاص أثناء مداهمة نفذها جيش الاحتلال الإسرائيلي عند أطراف مخيم جنين.
وقد حملت السلطة الفلسطينية وقناة الجزيرة إسرائيل مسؤولية استشهاد أبو عاقلة. وصرح مسؤول بارز في جيش الاحتلال في وقت لاحق من العام الماضي بأن هناك احتمالًا كبيرًا أن يكون قد أُطلق الرصاص عليها “بالخطأ من قبل جندي إسرائيلي، لم يكن، بطبيعة الحال، يعرف هويتها الصحفية”.